[微積分]tan x, sec x的積分 本題主要想解。 解:我們知道,所以如果令,則,因此原積分等於 。 請觀察 (1) (2) (1)與(2)相加之後可以得到: 如果我們令,則 如此一來 。 利用類似的想法,可以求出與 附註:如果是定義在實軸上某個區間內的可微分函數。我們記來表示。 其他做法: 利用 所以可推得 利用可知。於是 所以 利用 可以推得 利用 (與)可推得 我們知道 因此我們依然推得同樣的答案。
受用、感謝
附注第一,四,七条公式中的cos 应该改成 sin
Yes, 謝謝,您說的沒錯.
請問一下在一開始解tan x,令u=cos x那裡 能夠改成令u=sin x來解嗎?
也可以解
所以 1/2*sin^2(X)+C 也是此題的解摟?
可是為什麼用計算機帶值算出來會與原解有些許誤差呢?
因為你算錯了.
如果令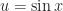 則
則 原來的積分要改寫為
原來的積分要改寫為
於是積分為
再利用部分分式解得
原來如此 謝謝