時間: Tue Jul 17 16:36:44 2007
本篇作於pttMath版
目的:希望提供一些學生微分方程方面的看法。
本文:
在此我想回答一些網友(非數學專業的)關於微分算子與微分方程的一些概念。微分方程的問題開始主要是來自於自然哲學(物理學),不管是常微分方程,或是偏微分方程。
假設表直點的位置與時間的關係,令
表速度與位置的關係,那麼一次以下的常微分方程
,
。
描述了物體的運動現象。隨著各類科學的發展,微分方程的內容也變得更多樣性了。從簡單的一次線性微分方程,發展到了高階非線性微分方程,通常我們可以用以下的微分方程來描述所有的常微分方程:
,
。
(可以是向量值,可以是純量)。而
是一個實值或向量值的函數(real-valued or vector valued functions)。我們必須思考,這樣的問題是否真的可以解?如果解本身是不存在的,那麼何來去解他呢?但,事實上,在微分方程的歷史中,剛開始數學家都是一股腦兒的用很多特殊的技巧去解方程,而非先證明解的存在性。然而,能夠用一些初等技巧解決的方程是少之又少。於是,數學家陷入了瓶頸。
在方程的歷史中,有一樣驚人的的創作,是出自於富利葉(Fourier)之手的,利用三角級數解決熱傳導的問題。當然,在那之前,數學家也思考用解析(冪級數)的方式去解微分方程的問題。Fourier的做法以現今數學觀點來看是相當不嚴謹的。然而,我們也不得不佩服他的獨創性。另外一個著名的工作就是出自於Volterra。Volterra利用方程的方法去研究生物生態學,(是他的一位好友讓他去研究義大利附近的海域魚群的生態)。接下來,微分方程漸漸地以一種專門的研究出現在數學的領域中。在那之前,數學家並不會專門的去研究方程,而是在致力於解決某一類的問題,如來自物理學的,來自於化學的,或是來自於幾何學等等的。
後來,Fredeholm研究積分方程提供了線性代數的方法解決積分方程的問題。這讓微分方程有了另外一種觀點(似乎並不是新的觀點)。當然在那同時期,恰巧是量子物理學正大肆橫掃古典物理的革命時期。積分方程,微分方程,到了Hilbert的手中,漸漸的融合成現今的泛函分析的起源。而解決微分方程,就用了線性代數的觀點,就是算子的概念。回到我們之前的問題。
首先我們必須考慮的是:我們想研究的函數是屬於麼樣的函數?連續?可微?時間的區間?解是否存在?如果我們把微分的過程視為由一個空間至另外一個空間的映射,那麼這樣的空間是屬於哪樣的空間呢?所有的可微分函數?連續的可微分函數?我們當然可以很簡單的說
是微分算子
的preimage,但是,那必須在一個前提之下,
所定義的空間被決定。當然
所定義的空間仰賴於我們所希望研究的空間。(註:利用泛函分析的方法並不是唯一研究方程的方法,而是他提供了一套有系統的研究方法)。因為,並不是任何的空間對我們來說都是有意義的。這也是為何會利用到Hilbert空間,或是Banach空間的理由。因為在量子物理中,粒子所存在的空間就是Hilbert空間
,或是
。而微分算子所定義的空間就是所謂的Sobolev空間。
的意義就給的更清楚了。然而在解方程的過程中,如給定
是連續函數
,
。
那麼微分算子(泛函分析)並不是一個簡單的方式去解決這樣的問題,而且是更加的複雜。(對某些問題來說),而一般工程數學上所謂的指的並不是微分算子,所謂的符號數學(Symbolic math)。利用某些觀念,或是符號可以幫助我們去解決問題,就如同前面有網友說的heaviside function或是Dirac function。其實在數學裡面,他的背景就是Distribution theory。而這正是Schwartz拿fields medal的得意之作。他們並不是不嚴謹,而是他們的背景並不是很容易,如果避掉了這些理論,用符號運算去解決方程,的確是一個方便的工具。
可以問一下老師嗎
n<2010, n可表示成六十個以上連續正整數相加,這樣的n有幾個?
你可以假設首項為 ,由於有
,由於有 項,所以最後一項為
項,所以最後一項為 。由連加的公式可知
。由連加的公式可知 。因此
。因此 。所以
。所以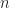 必為
必為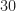 的倍數。由此你再想想看可以怎麼做,基本上就是討論
的倍數。由此你再想想看可以怎麼做,基本上就是討論 有幾組解囉!加油。給個提示
有幾組解囉!加油。給個提示 。
。
“如果我們把微分的過程視為由一個空間至另外一個空間的映射,那麼這樣的空間是屬於哪樣的空間呢?"
“heaviside function或是Dirac function。其實在數學裡面,他的背景就是Distribution theory。而這正是Schwartz拿fields medal的得意之作。"
thanks a lot, now I have a much better picture of Dirac function, and qm math.
“如果我們把微分的過程視為由一個空間至另外一個空間的映射,那麼這樣的空間是屬於哪樣的空間呢?" very good, 泛函分析 as a “system".
Distribution theory
基本理念
很多时候,函数是描述某个对象的性质的手段。传统的函数是将输入值和输出值建立对应关系的映射,是从本质上描述对象性质的方法。分布的概念则源自物理学的发展。二十世纪初发展起来的量子力学理论,特别是不确定性原理的发现,使物理学家抛弃了从本质上确定地表述对象的想法,而是将对象的性质视作它在一定的测量手段下的表现。我们能够获得“某个粒子的位置”的信息,是因为使用了某种测量的工具。对象的性质通过测量才得以表现。分布理论发展了这种概念,通过观察某个函数f与其它函数的“相互作用”来刻画这个函数。具体来说,我们观察f和一群“测量函数” 之乘积的积分:
之乘积的积分:
之所以使用积分作为“观察”的方式,一方面是因为在积分和求导两种数学分析的基本概念之间,(局部)可积分的函数比(局部)可导的函数要“多得多”;另一方面,则可以用物理上的测量方式解释。测量某个物理量的时候,我们往往不要求(也无法做到)知道此物理量在某个精确时刻或某个精确位置上的值,而只能通过多次测量,知道它在某一小段时间段或某个小区域内的平均测量值。从实际的角度,这种平均值才是测量和使用函数的最常见方式。而积分则是这种“平均值”的数学表现形式。
分布理论的目的在于建立一种比一般的函数更广泛的“广义函数”,称为分布,并能将微积分的常用结论运用到这类广义函数上去。
如果取 是所有
是所有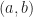 區間上
區間上 次可維的實值(或複值)函數。那麼一次微分
次可維的實值(或複值)函數。那麼一次微分 就是
就是
上的線性算子。