[數學物理]鏡象對稱原理

鏡象對稱原理的起源

假設 $X$ 是複數域上的光滑影射代數簇(smooth complex projective variety)．以解析拓樸(complex analytic topology)來說， $X$ 是一個光滑複流形．假設 $\dim X=d.$ 如果 $K_{X}=\Lambda^{d}\Omega_{X}^{1}\cong\mathcal{O}_{X}$ ，我們稱 $X$ 為Calabi-Yau代數簇(Calabi Yau variety)．

由於 $X$ 是影射光滑代數簇， $X$ 也會是Kahler流形．（因為影射空間是Kahler流形，Kahler流形的子流形均是Kahler）．我們令 $\omega$ 表示 $X$ 上的Kahler形．又條件(1)讓我們得知 $X$ 在全域上有全純的 $d$ 形式(holomorphic $d$ -form)，我們記 $\Omega\in H^{0}(X,K_{X})$ ．我們使用 $(X,\omega,\Omega)$ 來記Calabi-Yau代數簇．也就是說，要描述一個Calabi-Yau代數簇，我們必須要有(a)光滑影射代數簇 $X$ (b) Kahler形 $\omega$ (c) $X$ 上的全純 $d$ 形式 $\Omega$ ．

令 $\Omega_{X}^{*}=\Omega^{*}(X)\otimes_{\mathbb{R}}\mathbb{C}$ 表示 $X$ 上的全純複微分型所構成的層。我們令

$H^{p,q}=H^{q}(X,\Omega_{X}^{p})$

表示 $\Omega_{X}^{q}$ 的第 $p$ 個Cech同調群。

定理: (Hodge分解定理)如果 $(X,\omega)$ 是緊緻Kahler流形，則

(1) $H^{r}(X)=\bigoplus_{p+q=r}H^{p,q}$

(2) $H^{p,q}=\overline{H^{q,p}}.$

我們記 $h^{p,q}=\dim H^{p,q}(X)$ 稱為Hodge數。則我們可以用圖來表示 $h^{p,q}$ (稱為 Hodge diamond)。舉例來說物理學家研究 $3$ 維的Calabi-Yau代數簇的Hodge diamond時發現了一個奇特的現象。任給一個Calabi-Yau $X$ ，似乎存在另外一個Calabi-Yau代數簇 $X^{\vee}$ (但不唯一)使得 $h^{1,1}(X^{\vee})=h^{2,1}(X)$ 且 $h^{2,1}(X)=h^{1,1}(X)$ 。換句話說，如果我們看 Hodge diamond，那些數字剛好是沿著 $45^{\circ}$ 線的鏡像:如下圖

我們稱 $(X,X^{\vee})$ 為鏡像配對(Mirror pair)。而 $h^{p,q}$ 本身是具有幾何意義的。利用Kodaira-Spencer變形理論我們知道複結構 $J$ 的局部變形是由同調群 $H^{1}(X,TX)$ 所掌控(在這裡 $TX$ 記為tangent sheaf)。利用Serre duality我們知道

$H^{1}(X,TX)\cong H^{2}(X,TX^{\vee}\otimes K_{X})$ 。

由於 $X$ 是Calabi Yau，所以 $K_{X}\cong\mathcal{O}_{X}$ 。由於 $TX^{\vee}=\Omega_{X}^{1}$ 所以

$H^{1}(X,TX)\cong H^{2}(X,\Omega_{X}^{1})$ 。

因此 $\dim H^{1}(X,TX)=h^{2,1}$ 。於是這樣的觀察就開啟了鏡象對稱原理的研究．在陳述鏡相對稱原理之前，我們先來定義什麼叫 $A$ -model什麼叫 $B$ -model. 給定任何一個3維Calabi-Yau 代數簇 $(X,\omega,\Omega)$ （以下均簡稱為Calabi-Yau空間）

$A$ -model: $(X,\omega)$ 定義出來的Gromov-Witten不變量．

$B$ -model: $\Omega$ 的週期．也就是說任給 $3$ -cycle $\gamma\in H_{3}(X,\mathbb{Z})$ ， $\displaystyle\int_{\gamma}\Omega$ 稱為週期(period)．

鏡相對稱原理1.0:假設 $(X,X^{\vee})$ 是鏡像配對，則

(1) $X$ 的 $A$ -model對應於 $X^{\vee}$ 的 $B$ -model.

(2) $X$ 的 $B$ -model對應於 $X^{\vee}$ 的 $A$ -model.

範例2. $X$ 是複阿貝爾代數簇時， $X$ 是Calabi Yau，如橢圓曲線就是一例。

範例3. 所謂的 $K3$ 是二維(複數維度)且不為阿貝爾代數簇的Calabi-Yau。取四次的齊次多項式 $p(x_{1},x_{2},x_{3},x_{4})\in\mathbb{C}[x_{1},\cdots,x_{n}]$ 。如果 $X=\{p(x)=0\}$ 是光滑的，則 $X$ 定義出 $\mathbb{P}^{3}$ 中的ㄧ個 $K3$ 曲面。

範例4. 我們取五次齊次多項式 $q(x_{1},x_{2},x_{3},x_{4},x_{5})\in\mathbb{C}[x_{1},\cdots,x_{5}]$ ，我們可以定義出 $\mathbb{P}^{4}$ 中的超曲面 $X=\{q(x)=0\}$ 。這個超曲面稱為quintitic threefold(不知道怎麼翻譯比較好)。

後來 Kontsevich提出了以下的同調鏡象對稱原理。

同調鏡象對稱原理Homological Mirror symmetry principle.

如果 $(X,\omega)$ 是辛流形， $L$ 是 $X$ 的子流形並且 $\dim_{\mathbb{R}}L=\dim_{\mathbb{C}}X$ 且 $\omega|_{L}=0$ 我們稱 $L$ 是 $X$ 的Lagrangian 子流形。

$X$ 的Fukaya 範疇，記為 $\mbox{Fuk}(X)$ ，是由以下所組成的範疇:

(1)成員: $X$ 中的 Lagrangian 子流形。

(2)態射: $\mbox{Hom}(L_{1},L_{2})=HF^{*}(L_{1},L_{2})$ 是Floer homology groups。

假設 $\mathcal{A}$ 是一個阿貝爾範疇，我們用 $D^{b}(\mathcal{A})$ 來表示由 $\mathcal{A}$ 所構成的derived category。由於 $\mbox{Fuk}(X)$ 是一種所謂的 $A_{\infty}$ -category， $D^{b}(\mbox{Fuk}(X))$ 可以被定義。所以我們可以來描述同調鏡射猜想了。

同調鏡射猜想: (Kontsevich)如果 $(X,X^{\vee})$ 是一個Mirror pair，則

$D^{b}(\mbox{Fuk}(X))=D^{b}(\mbox{Coh}(X^{\vee}))$ 。

其中 $\mbox{Coh}(X)$ 為所有 $X$ 上的coherent sheaves所構成的範疇。

相關閱讀:

(1) Calabi 猜想

(2)古典力學與辛流形

(3)Kontsevich，MPI一生的轉捩點。

(4)Kahler 流形與Hodge分解(還沒寫)

(5)Derived Category (還沒寫)

[數學物理]鏡象對稱原理有 “ 5 則迴響 ”

david 說道：

03/08/2013 於 11:22 下午

“流形。如果是一個閉且非退化的二次微分型(closed two form, nondegenerate)"
first of all, thanks for your writings.

now, my question: not all 流形 are “非退化的二次微分型", what are those type of 流形 with “退化"? or not “as good as" 辛流形?

回應
1. frankliou 說道：
  
  03/09/2013 於 10:59 上午
  
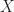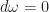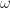  two form指的是定義在manifold $X$ 上，局部長的像 $\omega=\omega_{ij}dx^{i}\wedge dx^{j}$ 的"函數"(更正確的來說是截面)。當 $d\omega=0$ 時，我們稱 $\omega$ 叫closed。非退化是說矩陣 $(\omega_{ij})$ 行列式不等於零。而辛流形指的是 $(X,\omega)$ 這樣的東西，換句話說，他是光滑流形上負與辛結構的幾何空間。具有辛結構的流形必須要是偶數維，所有奇數維的流形，均不可能賦予辛結構。而偶數維的流形也都不是辛流形，分類辛流形的數學工作至今應該還沒完成。
  
  回應
2. frankliou 說道：
  
  03/09/2013 於 11:03 上午
  
  而你的問題並不是很make sense。因為所謂的"good"這定義並不清楚。
  
  回應
david 說道：

03/09/2013 於 5:34 下午

“good", I mean more linear, more classical measure, more like math/ for 经典力学, I will read your 古典力學與辛流形

回應
1. frankliou 說道：
  
  03/09/2013 於 5:57 下午
  
  您可以使用的簡體中文沒關係，我看得懂。:)
  
  回應