[幾何]古典力學與辛流形

古典力學與辛流形

假設 $\mathbb{R}^{2}$ 的座標用 $(x,p)$ 來表示。我們可以定義一個two-form為

$\omega=dx\wedge dp.$

並且 $d\omega=0$ 。如果用標準基底來表示，這個two form可以寫成矩陣的形式 $\left(\begin{matrix}0 & 1\\ -1 &0\end{matrix}\right)$ 這個矩陣的行列式為 $1$ ，所以我們知道這矩陣是可逆矩陣。事實上，我們把 $\mathbb{R}^{2}$ 看成是粒子的相空間。 $x$ 是粒子的座標函數， $p$ 是粒子的動量函數。 $\mathbb{R}$ 是一維的流形，他的切叢 $T\mathbb{R}$ 與 $\mathbb{R}^{2}$ 同構。而切叢正是粒子的相空間。(切叢主要是以位置與向量 $(x,v)$ 所構成的。如果粒子的質量為 $m$ 則動量為 $p=mv$ )。如果 $f,g:\mathbb{R}^{2}\to\mathbb{C}$ 是光滑函數，我們定義

$\displaystyle\{f,g\}=\frac{\partial f}{\partial x}\frac{\partial g}{\partial p}-\frac{\partial f}{\partial p}\frac{\partial g}{\partial x}.$

我們稱 $\{f,g\}$ 是 $f,g$ 的Poisson bracket。令 $V(x)$ 表示粒子的潛能函數。

說明:如果我們記 $\displaystyle\omega^{-1}=\frac{\partial}{\partial x}\wedge\frac{\partial}{\partial p}$ ，則用定義可知:

$\displaystyle\omega^{-1}(df,dg)=(\frac{\partial}{\partial x}\wedge\frac{\partial}{\partial p})(df,dg)=\{f,g\}$

令 $\displaystyle E_{k}=\frac{p^{2}}{2m}$ 表示粒子的動能，而位能為 $V(x)$ ，則粒子的總能量可以表達為

$\displaystyle H=\frac{p^{2}}{2m}+V(x),$

我們發現

$\displaystyle\{x,H\}=\frac{\partial H}{\partial p}=\frac{p}{m}=v=\dot{x}$ 且 $\displaystyle\{p,H\}=\frac{\partial H}{\partial x}=\frac{\partial V}{\partial x}=-\dot{p}$

其中我們使用到了牛頓方程 $\displaystyle m\ddot{x}=-\frac{\partial V}{\partial x}.$ 。更一般的，如果 $F(x,p,t)$ 是 $x,p,t$ 的函數，則經過計算後我們得到

$\displaystyle\frac{d}{dt}F(x,p,t)=\frac{\partial F}{\partial x}\frac{\partial H}{\partial p}-\frac{\partial F}{\partial p}\frac{\partial H}{\partial x}+\frac{\partial F}{\partial t}=\{F,H\}+\frac{\partial F}{\partial t}.$

所以如果 $F(x(t),p(t),t)$ 是常數函數，我們知道 $\dot{F}=0$ 。因此我們可以推得

$\displaystyle \frac{\partial F}{\partial t}=-\{F,H\}.$

定義:假設 $M$ 是一個 $2n$ 維的光滑流形。假設存在一個two form $\omega$ 使得 $d\omega=0$ 並且每點附近都存在局部座標系使得 $\omega$ 的矩陣表示為

$\left(\begin{matrix}0 & I_{n}\\ -I_{n} &0\end{matrix}\right),$ (*)

其中 $I_{n}$ 是 $n$ 階單位方陣。我們稱 $(M,\omega)$ 是一個辛流形。換句話說，取了局部座標系 $(x_{1},p_{1},\cdots,x_{n},p_{n})$ 後， $\omega$ 可以改寫為 $\sum_{i}dx_{i}\wedge dp_{i}.$ (這樣的座標系稱為Darboux座標系)

範例:假設 $X$ 是一個光滑流形，則 $T^{*}X$ 是一個辛流形。如果 $(x_{1},\cdots,x_{n})$ 是 $X$ 上的一個局部座標，令 $\psi(x_{1},\cdots,x_{n},p_{1},\cdots,p_{n})=p_{1}dx_{1}+\cdots+p_{n}dx_{n}$ 。則 $\psi$ 給出了 $T^{*}X$ 上的局部座標系。我們考慮 $\omega=\sum_{i}dp_{i}\wedge dx_{i}$ ，則 $\omega$ 給出了 $T^{*}X$ 上的辛結構。

如果我們令 $C^{\infty}(M,\mathbb{C})$ 表示所有的 $M$ 上光滑複值函數所成的代數。任給每點，取局部座標系後使得 $\omega$ 的矩陣表示為(*)，我們定義

$\displaystyle\{f,g\}=\sum_{i=1}^{n}\left(\frac{\partial f}{\partial x_{i}}\frac{\partial g}{\partial p_{i}}-\frac{\partial f}{\partial p_{i}}\frac{\partial g}{\partial x_{i}}\right).$

我們稱 $\{f,g\}$ 是 $f,g$ 的Poisson bracket。

命題: $C^{\infty}(M,\mathbb{C})$ 在 $\{\cdot,\cdot\}$ 的定義下構成一個無窮維的李代數。

如果 $N$ 是辛流形 $(M,\omega)$ 的子流形，並且 $\omega|_{N}$ 給出了 $N$ 上的一個辛流形，我們稱 $(N,\omega|_{N})$ 是 $(M,\omega)$ 的一個辛子流形。如果 $N$ 是 $M$ 的ㄧ個辛子流形，並且 $\omega|_{N}=0$ 我們稱 $N$ 是一個isotropic子流形。如果isotropic子流形的維數剛好是 $n=\dim M/2$ ，我們稱此isotropic子流形為Lagrangian子流形。

辛流形的量子化—量子物理

辛流形的量子化有點複雜，在此我只會談 $M=\mathbb{R}^{2}$ 的情況。令 $L^{2}(\mathbb{R})$ 表示所有實軸上平方可積分的函數所構成的Hilbert空間。令 $\mbox{Her}(L^{2}(\mathbb{R}))$ 表示所有 $L^{2}(\mathbb{R})$ 上的Hermitian算子所構成的空間。(我們可以取 $D$ 是 $L^{2}(\mathbb{R})$ 上的稠密子集，考慮 $D$ 上的Hermitian算子所構成的李代數， $[A,B]=AB-BA$ )。量子化就是一個李代數的同態

$C^{\infty}(\mathbb{R},\mathbb{C})\to\mbox{Her}(L^{2}(\mathbb{R})).$

其中，我們把 $x$ 送到乘法算子 $\hat{x}$ 把 $p$ 送到微分算子 $\hat{p}$ 定義如下:(附註，我們把Planck常數記為 $1$ 。)

$\displaystyle(\hat{x}\psi)(x)=x\psi(x),$ $\displaystyle (\hat{p}\psi)(x)=-i\frac{d\psi}{dx}.$

那麼 $[\hat{p},\hat{x}]=-i$ 。於是能量函數(Hamiltonian)就變成

$\displaystyle \hat{H}=\frac{\hat{p}^{2}}{2m}+\hat{V}.$

如果寫成微分的形式就是:

$\displaystyle \hat{H}=-\frac{1}{2m}\frac{d^{2}}{dx^{2}}+V(x).$

所以薛丁格方程就是以下的偏微分方程:

$i\displaystyle\frac{\partial\psi}{\partial t}=\hat{H}\psi.$

但當 $M$ 是更一般的辛流形時，量子化就變得更複雜了。我們有機會在談。而薛丁格方程的解，咱們有機會再談。

[幾何]古典力學與辛流形有 “ 21 則迴響 ”

chiushengfu 說道：

09/24/2012 於 12:26 下午

量子化的出發點很直觀，但是實際操作的話會遇到後面高階的項湊不攏的問題。為了解決這個問題，演化出眾家量子化方案….XD

回應
1. frankliou 說道：
  
  09/24/2012 於 1:07 下午
  
  這就是目前量子化的問題。沒有"canonical"的選擇。
  
  回應
引用通告： [數學物理]鏡象對稱原理 | 法蘭克的數學世界
david 說道：

03/09/2013 於 6:03 下午

1. “圆是除欧几里得空间外的拓扑流形的一个简单例子。让我们考虑一个半径为1，圆心在原点的圆。若和是圆上的点的坐标，则有。

局部看来，圆像一条线，而线是一维的。换句话说，我们只要一个坐标就可以在局部描述一个圆。例如，圆的上半部，坐标大于零的部分（右图中黄色的部分），任何一点都可以用坐标确定。投影映射：把上半圆映射到开区间。反过来，给定一个，就是上半圆的一点：这样的一个映射就是一个坐标图。它的作用，就是告诉读者“地图”上的一点对应着实际中的哪一点。和它的逆映射都是连续函数甚至是光滑函数，这样的映射也叫做一个（微分）同胚

[1]:4。类似的，也可以为圆的下半部（红），左半部（蓝），右半部（绿）建立坐标图。这四个部分合起来覆盖了整个圆，这四个坐标图就组成了该圆的一个图册。"
-wiki
http://zh.wikipedia.org/wiki/%E6%B5%81%E5%BD%A2
2″事實上，我們把看成是粒子的相空間。是粒子的座標函數，是粒子的動量函數。是一維的流形，他的切叢與同構。""2″ is very much like or examplified by “1″, making sense? in terms of better “measue" and/or better “可定向性"as compared to 莫比乌斯带 [编辑] 莫比乌斯带从一个竖着的无限圆柱面开始，这是一个无边界的流形。

回應
1. frankliou 說道：
  
  03/09/2013 於 6:20 下午
  
  粒子的相空間是切叢沒錯。(或者是餘切叢，這兩者同構)莫比烏斯帶是不可定向的流形。辛流形是可定向的，因為辛結構會給予辛流形方向性。如果以數學的語言來說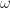， $\omega$ 如果是辛結構 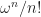$\omega^{n}/n!$ 給出了volume form (體積型)通常可定向讓流形上面可以有良定的積分概念，換句話說，給了你測量"體積"的概念。
  
  回應
david 說道：

03/09/2013 於 6:18 下午

http://blog.sina.com.cn/s/blog_486c2cbf0102e9fx.html
this guy’s post makes sense to me

回應
david 說道：

03/09/2013 於 6:48 下午

I’m going to define a mathematical object called a phase space. This is supposed to be a set of observable facts about a physical system (a “phase”); each point might represent a specific position and specific momentum, or it might be something coarser. Informally, we want that if we specify an energy function which only depends on the phase, then we can tell how the phase evolves with time, and this evolution is “reasonable.” More formally a phase space is a manifold equipped with the following structure

http://sbseminar.wordpress.com/2012/01/09/what-is-a-symplectic-manifold-really/

———
,
軌跡 of such an energy function can be said as “圆圈一维流形", classical system

————–
“丘成桐與卡拉比猜想60年", I kind of understand it a bit, could you write a more 科普 one when you have time? thanks

回應
1. frankliou 說道：
  
  03/09/2013 於 7:37 下午
  
  OK. I will try if I have time.
  
  回應
david 說道：

03/10/2013 於 4:56 下午

“Bourbaki的成員們一致同意以數學結構作為分類數學理論的基本原則。「數學結構」是Bourbaki的發明，他們認為，數學世界中有幾種基本的結構：代數結構、拓撲結構、序結構，這些結構經過混合和雜交，就得到數學的各種研究對象。比如實數集合，從代數結構看是一個域，從拓撲結構看是單連通(simply connected)的，從序結構(ordered structure)看是全序集(totally ordered set)。而拓撲群(topological group)則是拓撲結構與群結構結合而成。因此，數學的分類就是以結構來劃分，比如線性代數和初等幾何研究的是同一種結構，而歐氏幾何則是Hilbert空間在Hermitian算子作用下的特殊情形"

this is very good, and if you could expand it into a 科普 (wiki style or level) article when you have time, thx

回應
david 說道：

03/12/2013 於 3:20 上午

1.
“Calabi-Yau流形是一個緊緻且Ricci平坦的凱勒流形"众所周知，庞加莱（Poincare）著名的单值化定理告诉我们，一维复流形的万有覆盖只有简单的三种，球面、复平面和单位圆盘。如何将单值化定理推广到高维流形，这个问题几乎主导了现代几何与拓扑的发展。而即使从复一维到复二维流形，问题的复杂性已经远超想象，被数学家称作是从天堂到了地狱。或者说是上帝创造了黎曼面，简单美丽而又丰富多彩，是魔鬼制造了复曲面，内容复杂，令人眼花缭乱，头晕目眩。卡拉比猜想可以认为是单值化定理在高维不可思议的大胆推广，竟然给出了高维复流形中难得一见的一般规律。特别的是它在复卡勒流形的第一陈类大于零、等于零和小于零三个情形，指出了Kahler-Einstein度量的存在性，即此度量的第一陈形式等于其卡勒形式。这恰好对应于黎曼面三种单值化的推广

2.now, in Calabi-Yau流形: do we have some kind of “測量", like “volume form (體積型)通常可定向讓流形上面可以有良定的積分概念，換句話說，給了你測量"體積"的概念", which may be some how still 保體積?where dimensions could be 高维,

Eucid space:保长度;辛流形, 保體積;

Calabi-Yau流形:保 what?

thanks

回應
1. frankliou 說道：
  
  03/12/2013 於 8:05 上午
  
  A Calabi-Yau Manifold is a Kahler manifold. Of course, it has a volume form given by the Kahler form. I don’t understand your question"保體積"? Ususally, 保XX is a property of certain transformations and not a property of manifolds itself. 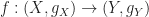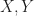For example, a smooth map $f:(X,g_{X})\to (Y,g_{Y})$ between Riemannian manifolds is conformal if there exists a positive smooth function $\lambda:X\to\mathbb{R}$ so that $f^{*}g_{Y}=\lambda g_{X}.$ If $X,Y$ are complex curves and 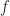$f$ is holomorphic, then 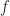$f$ is conformal; it is a result from complex analysis.
  
  回應
david 說道：

03/12/2013 於 3:37 上午

“如果一個完備流形的測地圓球體積增長不比二次增長更快，即

$\mbox{Vol}(B_r)\leq Cr^2$ ;

那麼這個流形上便不存在非常數的正值上調和函數"

按一下以存取 yau_2010_gradient_tims-Chinese.pdf

1974 年，我應用這種想法解決了一個幾何問題：在Ricci 曲率為正的完備非緊緻流形上，測地圓球體積之於半徑的增長是線性的。(在單射半徑(injectivity radius) 有一些限制的情況下，Calabi 也證明了同一命題。)接著鄭紹遠-李偉光-丘成桐在一篇關於熱核(heat kernel) 估計的文章中研究了測地圓球體積與單射半徑間的關係，之後又被Cheeger-Gromov 推廣。這一想法成為了許多後來與幾何有關的工作的基石，並且在Hamilton 與Perelman 的文章中都又出現了。基於這篇文章中的想法，我猜測在一個流形上，具有固定多項式增長率的調和函數全體是一個有限維的空間。後來這被Colding與Minicozzi 解決，李偉光與王嘉平接著做了一些改進。

鄭紹遠跟我提出的想法如下：首先證明，如果在Minkowski 空間上選定了適當的大域座標，那麼該超曲面的位置向量的Lorentzian 長度會是個正的恰當函數(proper function，意指緊緻集的原像亦為緊緻集)。然後，對此函數應用我們對調和函數所做估計的基本想法。在一些微妙之處必須再次用上極大超曲面方程式，不過我們終究找到了這個函數取log 值後的梯度估計在1983 年，我建議Hamilton 考慮利用Ricci 流證明Thurston幾何化猜想(geometrization conjecture) 的可能性，因為證明一個幾何結構的存在性最自然的辦法就是透過非線性微分方程。微分方程給出的形變(deformation) 的奇蹟，我們關於背景空間的拓樸不必知道得太多，這正是此途徑主要的優於Thurston方法之處。

Hamilton 以很多方式從跟均曲率流(mean curvature ow) 做類比得到關於他的Ricci 流的直觀。曲線縮短流(curve shortening flow) 已被Grayson 研究過，而Hamilton 因為對類比(analogy)的關心對此展現了極大的興趣。

$\displaystyle\frac{\partial F}{\partial t}=H=\Delta_{\Sigma} F$

緊接在那之後， Huisken 考慮了均曲率流中Hamilton 定理的類比：均曲率流將一個歐氏空間中的凸緊緻超曲面演化成一個圓球面。均曲率流中有很多自相似解，人們可以從它們學到一些東西。

回應
david 說道：

03/12/2013 於 9:06 下午

“保XX=保度量"” in my question; “保XX is a property of certain transformations and not a property of manifolds itself", thanks now,in “Calabi-Yau流形是一個緊緻且Ricci平坦的凱勒流形", what kind of 度量 they try to 保? thanks

回應
1. frankliou 說道：
  
  03/12/2013 於 9:44 下午
  
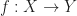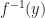  我用中文再說一次好了。保持甚麼"幾何性質"是必須要在光滑映射作用下才有意義，因為"保持XX"並不是流形本身的性質。Calabi Yau流形他就是Ricci(某一類的曲率)平坦的空間。因此，你的問題沒有任何意義。但你可以問說，如果給定一個複流形之間的全純映射 $f:X\to Y$ ，並且知道 $f^{-1}(y_{0})=X_{0}$ 是一個Calabi-Yau，在甚麼樣的條件下 $f^{-1}(y)$ 會全是Calabi-Yau。(Calabi-Yau空間的形變何時可以得到Calabi-Yau)。
  
  回應
david 說道：

03/13/2013 於 8:59 下午

“Calabi-Yau空間的形變何時可以得到Calabi-Yau"

thanks, looks like I have some wrong “concepts" in my mind

————
http://www.fxkz.net/forum.php?mod=viewthread&tid=175

原帖由星空浩淼于 2008-2-5 18:27 发表
在流形上，与局部坐标选取无关的“概念”，“性质”，和与局部坐标变换相容的“ 量”，才是有几何意义的。
－－－－－－－－－－－－－－－－－－－－－－－
这句话如果这样说可能更好理解（假如可以这样说的话）：只有保持拓扑变换不变的量（即微分同胚变换不变的量），才是有几何意义的。

有一些差别。这里不涉及任何对称性或者群作用。如果在每个局部坐标系 U 里有一组数据，当一个区域可以使用不同局部坐标 U, U’，而 U 里头的数据可以通过某种（依赖于局部坐标变换的）规则同 U’ 里的数据联系起来的时候，这组数据就组成了一个整体定义的量。这跟狭义相对论还是有所不同，在那里，时空是平直的，坐标系之间的变换同空间本身的 Poincare 群作用几乎可以对等，所以教材上面从来不区分是“坐标变换” 还是“点变换”。在流形上，坐标都是局部的，这种区别就很关键了。

回應
david 說道：

03/13/2013 於 9:08 下午

also, could you possibly have a table of contents ? I remember I have read one of your postings about 地球球心處重力場, or something similar?

thanks

回應
david 說道：

03/13/2013 於 10:38 下午

I hope I am not bothering you too much, and if you can tolerate my mix of english and chinese (4 faster typing), now

1. 环面的生成元不必是圆，而可以是椭圆或任何圆锥曲线,

http://zh.wikipedia.org/wiki/%E7%8E%AF%E9%9D%A2

2 环面 as a 哈密顿系统(such as 鐘擺的擺動,)’s 相空间,

3. 椭圆 as 軌跡 (將微分方程解之曲線) of 鐘擺的擺動

now 椭圆 here=一维辛流形, and 环面=切叢, (或者是餘切叢，這兩者同構),..

4.if we have many 哈密顿系统 or similar systems, and we would have “many"切叢,

and if we can find a 向量场 which can 联络 all these “切叢", then such a 向量场=規範場

conceptually, I am not too off the “track" of basic concepts?
(I am sure I have a lot of technical terms mistakes here)

—————-

按一下以存取 27205.pdf

book.hzu.edu.cn/485073.html – 轉為繁體網頁

根据经典的KAM定现,对于典型的近可积哈密顿系统,相空间的绝大部分被不变环面所充满,环面上的相流是拟周期运动.由此产生了一个自然的问题:在余下的相空间中 …

共振区的低维不变环面哈密顿系统

book.hzu.edu.cn/485073.html – 轉為繁體網頁

根据经典的KAM定现,对于典型的近可积哈密顿系统,相空间的绝大部分被不变环面所充满,环面上的相流是拟周期运动.由此产生了一个自然的问题:在余下的相空间中 …

回應
david 說道：

03/13/2013 於 10:47 下午

“流形M上相同階次的張量組成一個以 M為底的纖維叢(張量叢)，張量場是它的截面，切叢、余切叢、向量場、一次微分形式都是它們的特例。"切叢、余切叢、向量場都是張量場的特例,低dimension投影?thanks for spending your time answering my qestions

————-

http://art.tze.cn/Refbook/entry.aspx?bi=m.20080213-m300-w001-052&ei=5EE15FC2740914DF4051EEFCC1055ACA3B24CCE53D93AF91D9353EBD27775F32E3882DC11037C85F&p=42&cult=TW&Token=D6E79E7A374B9C1444B143738C4EF31F

回應
1. frankliou 說道：
  
  03/14/2013 於 10:27 上午
  
  我不知道你的問題是甚麼?
  
  回應
david 說道：

03/14/2013 於 12:22 上午

1. correction"环面 as a 哈密顿系统(such as 鐘擺的擺動,)’s 相空间, "
鐘擺的擺動=双摆的擺動
2. 单摆的擺動相空间 is not 环面, I think, what is it?

双摆中的混沌
course.bnu.edu.cn/course/jswl/files/xslw/…/bnu20.pdf – 轉為繁體網頁

檔案類型: PDF/Adobe Acrobat – 快速檢視轨道，是运动周期性的表现，说明了在小角度下看似复杂的双摆运动. 实际上是一个准 … 也就是说双摆运动的准周期轨道从局部开始逐渐的被破坏。 0. 1(0) 1 θ. = 0 …

回應
引用通告： [數學物理]鏡象對稱原理 | 法蘭克的數學世界